A Fairy Tail or The Magic of Extreme Casino Wins

Michael Shackleford, a who has made a career of analyzing casino games, designed Australian Reels Slot Machine in 2009. In modeling the casino's risk of ruin he (blindly) relied on the normal distribution. We show that this drastically undervalues the tail risk.

Although letYourMoneyGrow.com is the website for those, who play only games with a positive expectation, we are sure that this essay will be interesting for our readers. And not only from educational point of view; finally, there is a way to make money in casino: namely to be a casino's owner. An casino owner does have a positive expectation of the game. However, it is not enough: additionally, s/he has also to control the risk, which might be high.

A friend of mine wanted to implement the Australian Reels Slot Machine and asked me to validate his implementation according to the original paper. For your convinience we cite two key tables from this paper:

Pay Table
Win	1 coin	2 coins	3 coins
Three flags	8000	16000	25000
Blue 7, white 7, red 7 (in order)	1000	2000	3000
Three blue 7's	300	600	900
Three white 7's	200	400	600
Three red 7's	100	200	300
Any three 7's	40	80	120
Three kangaroos	40	80	120
Three platypuses	30	60	90
Three echidnas	20	40	60
Any three animals	2	4	6
Any three symbols	1	2	3

Return Table
Combination	Pays	Probability Combinations	Return Combinations	Probability	Return
Three flags	8333	1	8333	0.000004	0.031789
Blue 7, white 7, red 7	1000	11	11000	0.000042	0.041962
Three blue 7's	300	30	9000	0.000114	0.034332
Three white 7's	200	68	13600	0.000259	0.051880
Three red 7's	100	141	14100	0.000538	0.053787
Any three 7's	40	1249	49960	0.004765	0.190582
Three kangaroos	40	629	25160	0.002399	0.095978
Three platypuses	30	879	26370	0.003353	0.100594
Three echidnas	20	1439	28780	0.005489	0.109787
Any three animals	2	17729	35458	0.067631	0.135262
Any three symbols	1	32544	32544	0.124146	0.124146
Total		54720	254305	0.208740	0.970098

Further Mr. Shackleford writes:

The next three tables show the probability that the return of the game will fall between the specified markers and number of spins. For example, with one million spins there is a 95% chance that the return of the game will fall between 95.21% and 102.70%. It is beyond the scope of this document to explain how these were calculated, but any introductory statistics text will explain it under "confidence intervals".

95% Confidence Interval – Max Coins Bet
Spins	Lower Bound	Upper Bound
1000	40.16%	153.86%
10000	79.03%	114.99%
100000	91.32%	102.70%
1000000	95.21%	98.81%
10000000	96.44%	97.58%

From the quoted text one can infer that Mr. Shackleford relies on the normal distribution. This also can be formally checked, if you calculate the mean and variance of the game outcomes, input them as the Gaussian distribution parameters and calculate the 95% confidence interval.

But relying on the normal distribution is a big negligence! Look at Return Table: some combinations come though extremely rarely, their payoff is huge. And a casino has to offer such combinations, because gamblers subconsciously want to make a jackpot; smaller wins are much less exciting even if their probabilities are higher.

But extreme payoffs mean that one can (and should) expect heavy tails! Starting from one million spins the law of the large numbers does it job and cuts the tails, thus the normal approximation works well (although still not perfectly, as you can readily see from the highest and lowest quantiles in QQplot).

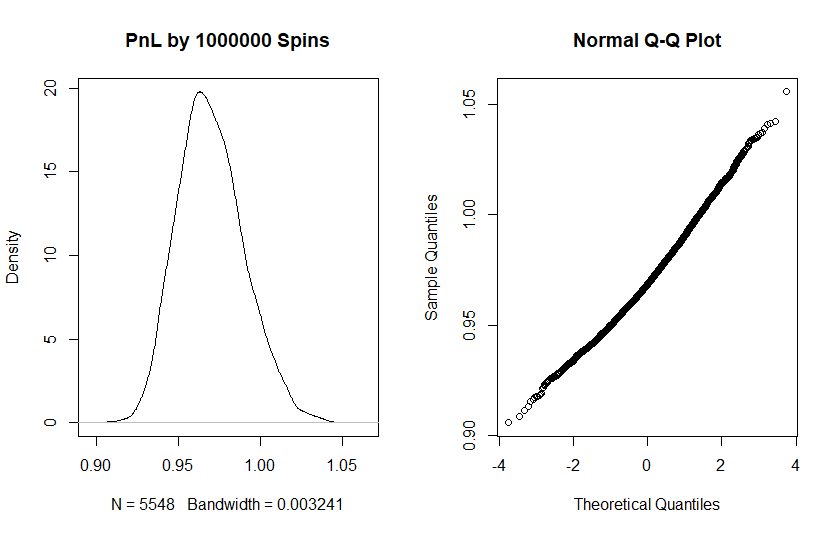
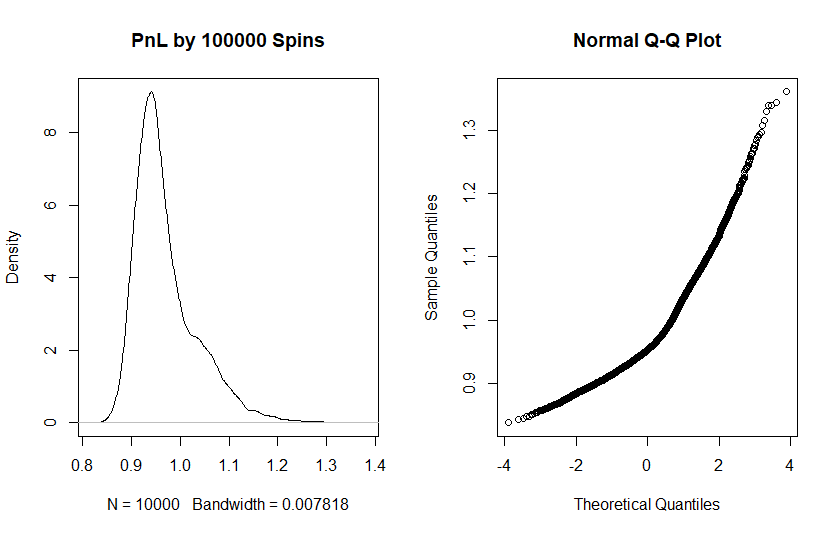
But already by 100 thousands spins the normal distribution works poorly.

And by 10000 rounds (which is realistic for a small casino) the tail risks are extremely high!
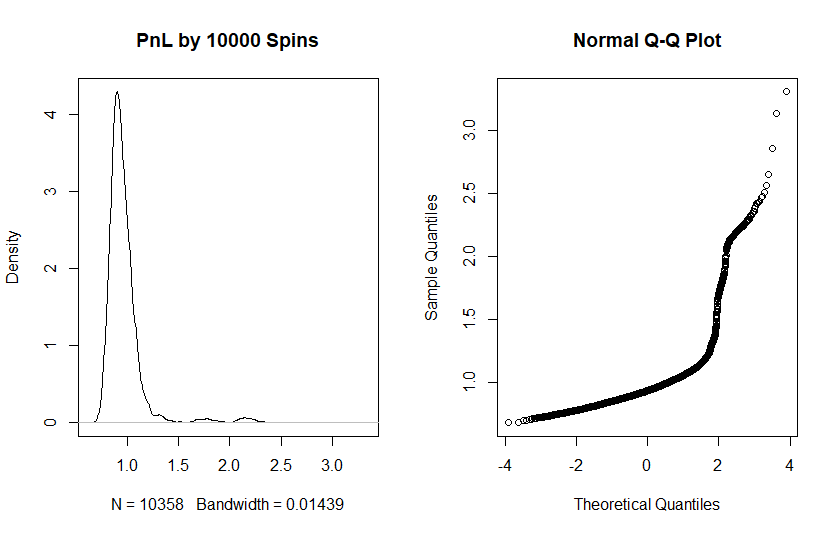The probability to make a loss, i.e. to have to pay more money than was encashed from gambles is above 10%! And in 1% of scenarios a casino has to pay more than double of what it has raked! And of course there are rent costs, taxes and so on! Thus a gambling business is not always a gold mine! Furthermore, if planned carelessly, it might go bankrupt!

So what is the moral of this essay? Is it relevant for casino owners only? No, it is relevant for everyone, who engages mathematical modeling (esp. in trading): Do check your assumptions by means of the Monte-Carlo simulation, it is easy, cheap and straightforward!

P.S.
By this essay we did not mean to ridicule Michael Shackleford. Rather, it is the case like When Genius Failed.

P.P.S.
Since we are not the owner of the implementation of Australian Reels Slot Machine, we cannot publish the complete program code here for the sake of reproducibility, as we usually do.
However, to give you a better idea of what data we have plotted above, we provide the code that we used to validate this Machine.

static void play(GameAustralianSlot machine,PrintWriter file){
		String currentLine;

		final int N_SCEN = 10000;
		final int N_ROUNDS = (int)100000;
		for(int scen=0; scen<N_SCEN; scen++)	
			try{
			for(int i=0; i<N_ROUNDS; i++) {
				
					Tx tx = new Tx(new BigDecimal(randInt(1, 3))); 
					if(tx.amount.signum() == 0 || tx.amount.compareTo(minStake) < 0 || tx.amount.compareTo(maxStake) > 0){ 
						continue; 
					}
					RoundResult rr = machine.play(tx.blockNum, tx.txHash, tx.from, tx.amount);
					
					totalRounds.incrementAndGet();
					winSum = winSum.add(rr.win);
					stakeSum = stakeSum.add(rr.stake);
										
				    }
					System.out.println(winSum.doubleValue() /stakeSum.doubleValue());
					file.println(winSum.doubleValue() /stakeSum.doubleValue());
					winSum = zero;     
					stakeSum = zero;
					
			} 	
		
			catch(Exception e){
				System.out.println("Oops, something goes wrong!");
			}
	}

Then the results are visualized in R as follows:

dat3 = read.csv(file="D:/sandbox2/slot/game.result.txt", header=FALSE, sep=";")
par(mfrow=c(1,2))
plot(density(dat3$V1), main="PnL by 100000 Spins")
qqnorm(dat3$V1)