Binary Options: you may earn in a short term but eventually you WILL lose

Summary: 

• Gambling with binary options you either lose 100% or earn about 90% of your stake. The win lose/ratio of 90/100 = 0.9 is worse than by the European roulette (36/37 = 0.973) and even by American roulette (36/38 = 0.947).
• A trade takes just a couple of minutes, which allows (and implicitly encourages) you to commit a lot of trades. Due to the law of large numbers and negative odds, the more you trade, the more you lose.
• Don't trust numerous "success stories" in Internet. Virtually all of them are fake and they are just a marketing trick of brokers or those who earn with brokers' affiliate programs.

I am frequently asked whether one can regularly make money with binary options. As I answer "regularly, you can only lose with binary options" they doubt and say something like "but there are so many videos of success stories on YouTube!..".
Well, to tell you a lie one even does not need to fake the video itself (which is also technically possible). All one has to do is just to record and present just one successful trade session. By the probability of both profit and loss equal to 50% and 100 trades (actually, "stakes" is a more appropriate word here) approximately a third of scenarios will be profitable. Is it reasonable to assume 50/50 probability?! The answer is yes! Sometimes you may guess the market direction with a higher probability but in most cases it is unpredictable, esp. by a very short time frame.  Here we have additionally assumed the win/lose ratio of 0.9 (it varies by brokers but 0.9 is a pretty good value).

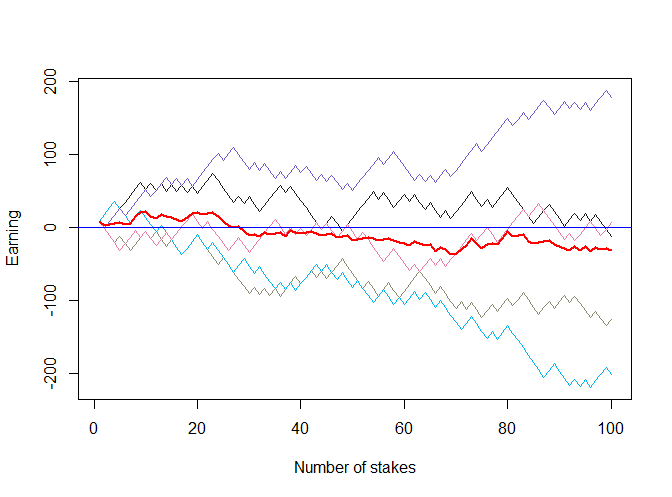
Moreover, as Figure 1 shows, it is not improbable that there will be a scenario, by which the total earning remains strictly positive (although you make losses by some trades).
You may reproduce Figure 1 with the following R code

PROB_WIN=0.50
PROFIT_RATIO = 0.90
STAKE_SIZE = 10.0
N_TRADES = 100
N_SCENARIOS = 5
outcomes = array(0.0, dim=c(N_TRADES, N_SCENARIOS))
meanOutcome = array(0.0, dim=N_TRADES)
for( i in 1:N_SCENARIOS)
{
    trades = rbinom(N_TRADES, 1, PROB_WIN)
    trades[which(trades==1)] = PROFIT_RATIO * STAKE_SIZE
    trades[which(trades==0)] = -STAKE_SIZE
    outcomes[,i] = cumsum(trades)
    meanOutcome = meanOutcome + outcomes[,i] / N_SCENARIOS
}
ts.plot(outcomes, xlab="Number of stakes", ylab="Earning", col = sample(colours(), N_SCENARIOS))
lines(meanOutcome, col="red", lwd=2)
abline(h=0, col="blue")
print("your earning are profitable in: " )
print(paste(length(which(outcomes[N_TRADES,]>0)), "of", N_SCENARIOS, "cases"))

Since the outcomes are random, you will get a different picture each time you run this code. However, there will be at least two similarities: there will usually be more lossy than profitable scenarios and, respectively, the fat red line, which averages the outcomes over all scenarios, will drop below zero.

Still, although the odds are against you, the probability to make profit is about 30% and with some extra luck the profit may be good. But look what happens if we increase the number of stakes in scenario to 5000! To make our simulation exhaustive we also increase the number of simulated scenarios to 500 (just set N_TRADES = 5000 and N_SCENARIOS = 500 in R code above).

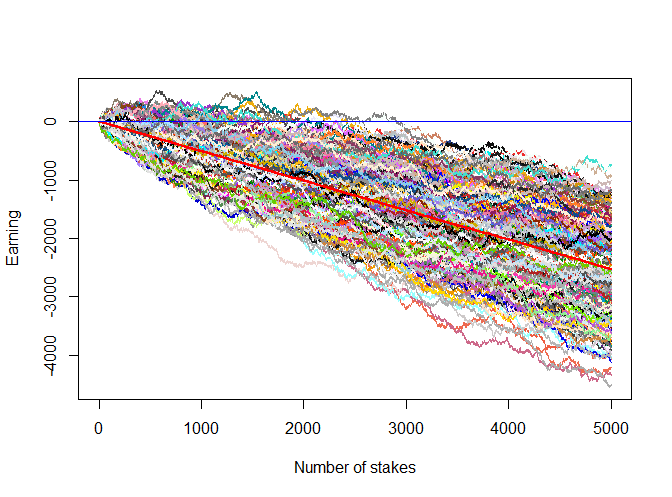
As Figure 2 shows, if you commit more than 3000 trades, you surely lose!

Thus hands off from binary options!

P.S.
1) here we assumed that each time a trader (better to say "a gambler") bets a fixed amount of money. But usually he tends to increase the stakes if his capital (temporarily) grows. In this case he gets broke even more quickly (we will discuss this phenomenon in following posts).
2) Don't confuse binary from bucket shop with genuine binary options that are traded on exchanges.