Mystery and misery of the martingale betting system: why it will not make you rich

Summary:

• The martingale strategy asymptotically implies infinite capital or infinitely divisible stake. In reality you have a limited capital and there is a lower (in casino also an upper) bound of the stake.
• In a fair game (with 50/50 chance of profit and loss) the probability of profit after a series of losses is still 50% (because the outcomes of bets or trades are independent from each other).
• Typically, if you win then your profits are moderate but if you lose, the losses are severe (you can lose your capital just after a small series of unlucky bets).
• If you make pretty many bets, you might make a good profit but the probability to make profit at all decreases with the number of bets. Losses stays severe.

Internet scammers that try to lure you to bet in online casino or gamble with binary options frequently claim that you can surely win with the so-called martingale strategy:
1) start betting with the minimal stake
2) if you lost by the previous bet then double the stake, and set it again to minimum as soon as you win.

Let's assume that a trader has $10000 trading capital and the minimal stake is $100 (less is not worthy due to fixed broker fees and our trader does not want to waste his time with penny stakes). At first we simulate only five scenarios in order to keep Figure 1 legible and get a "qualitative impression" of what may happen.

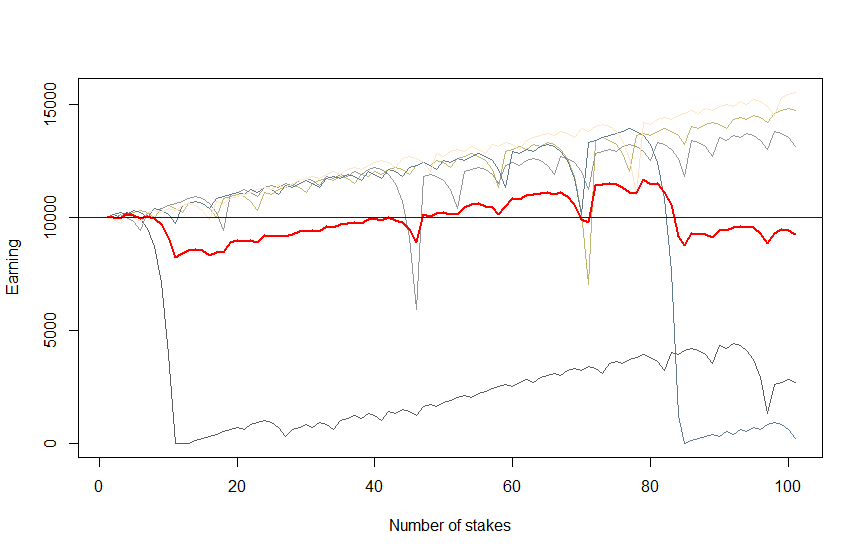
You see that there are three scenarios with moderate profits and two scenarios with heavy losses. Figure 1 was created with the following R-code. Note that before doubling the stake after a loss we check (code lines 23-28) whether we have enough money for it. If not, we stop trading (and freeze the remained capital) and proceed to the next scenario.

PROB_WIN=0.5 #fair game with 50/50 chances
INIT_STAKE = 100.0 #due to brokers fee it is usually not worth betting less than $100
INIT_CAPITAL = 10000.0 #a plausible trading capital amount for a retail investor
N_TRADES = 100
N_SCENARIOS = 5
outcomes = array(INIT_CAPITAL, dim=c((N_TRADES+1), N_SCENARIOS))
meanOutcome = array(0.0, dim=(N_TRADES+1))
for( i in 1:N_SCENARIOS)
{
    trades = rbinom((N_TRADES+1), 1, PROB_WIN) 
    stake = INIT_STAKE
    for(k in 2:(N_TRADES+1))
    {
        if(trades[k] == 1) #if won, set the stake to initial (minimal) value
        {
            outcomes[k,i] = outcomes[(k-1),i] + stake
            stake = INIT_STAKE 
        }
        else #if lost, double the stake but check whether you have enough money!
        { 
            outcomes[k,i] = outcomes[(k-1),i] - stake
            stake = min(2*stake, outcomes[k,i]) 
            if( (outcomes[k,i] <= 0.0) || (stake < INIT_STAKE))
            {
                outcomes[(k:(N_TRADES+1)), i] = max(0.0, stake)
                stake = INIT_STAKE #set it to minimum before proceeding to the next scenario
                next #if you lost and cannot double the stake, abandon this and go to the next scenario
            }                 
        }
    }

    meanOutcome = meanOutcome + outcomes[,i] / N_SCENARIOS
}
colorz = sample(colours(), N_SCENARIOS, replace=TRUE)
ts.plot(outcomes, col=colorz, xlab="Number of stakes", ylab="Earning", gpars=list(yaxt="n"))
myTicks = axTicks(2)
axis(2, at = myTicks, labels = formatC(myTicks, format = 'd')) 
lines(meanOutcome, col="red", lwd=2) #averaging among all scenarios
abline(h=INIT_CAPITAL, col="blue")
print("your earning are profitable in: " )
print(paste(length(which(outcomes[(N_TRADES+1),] > INIT_CAPITAL)), "of", N_SCENARIOS, "cases"))

Since the outcomes are random, you get a different graph if you run this code. However, likely there will still be moderate profits and heavy losses (try to run the code several times). Now let us set N_SCENARIOS = 1000 in order to make our simulation statistically significant.

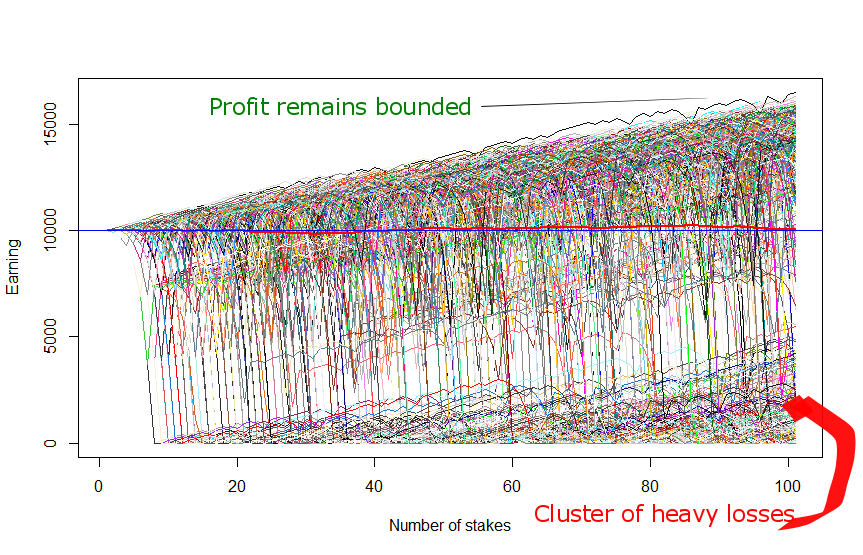
By N_SCENARIOS = 1000 approximately 2/3 of them end up with profit (since now we simulate a lot of scenarios, the ratio 2/3 will only slightly fluctuate if you re-run the R-code several times). But the profitable scenarios are bounded (even in the best case you hardly earn more than 60% on traded capital). And there is a distinct cluster of severe losses in the bottom corner!

Finally, let us increase the number of trades setting N_TRADES = 1000 but reduce the number of scenarios setting N_SCENARIOS = 30 (otherwise we will hardly distinguish the lines on the graph).

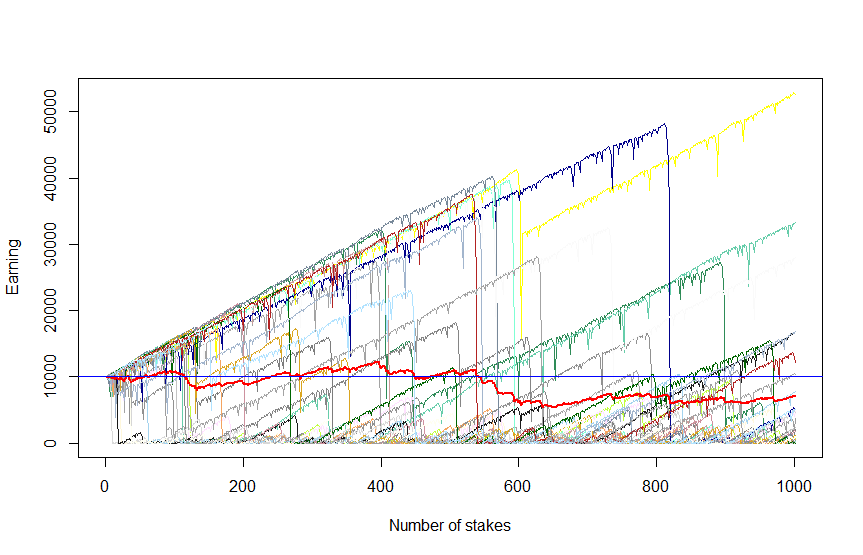
We see that though now there are some scenarios with really high profit, they are more occasional now (indeed there only 1/3 scenarios with profit). Esp. the dark-blue scenario justifies its colour, making us so blue: we had made more than 300% profit and then lost everything just after a couple of unlucky trades!
In order to keep the integrity of our review we also provide Figure 4, which shows (red thick line) that the in expectation, i.e. on average among all scenarios, the profit does grow (in Figure 3 it decreases but it is accidentally and statistically insignificant since we have only a few scenarios).

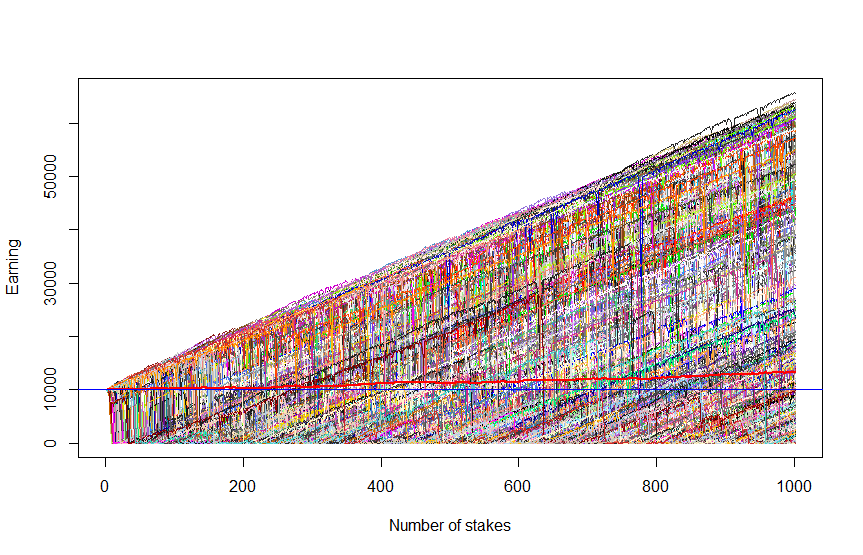
However, the growing expectation brings us little comfort since it grows exclusively due to extremely good scenarios that become extremely rare as the number of trades grows (recall: you can lose your capital just after a few of consequent unlucky bets).
Finally, let's do some math to make everything clear.

1. If you bet only once the probability to win is . If you bet twice, the probability to win at least once is since the possible outcomes are WW, WL, LW and LL. Generally, if you bet times, it is easier to consider at first the probability to always lose, it is equal to .  Respectively, the probability to win at least once is equal to . Thus if you are going to make a series of five bets, you win at least once with probability . But if you already made four bets, the probability to win (or lose) by the 5th bet is ... because the bets are serially independent and the outcomes from the past are irrelevant for the future! Yes, it may sound counter-intuitive but if you doubt, do the homework: make at least 100 series of 5 coin tosses (so totally you have to toss a coin 500 times) and look whether the result of the 5th toss depends on the previous four...Of course the situation changes when the outcomes are serially dependent. For example, if you trade a commodity, sooner or later its price will rebound. For instance, it happened to the crude oil  in the beginning of 2016: first it dropped below $30 but then jumped over $50 (however, don't expect this with a single stock, since companies do lose there market share and do go bankrupt).
   Another example: according to the law, the casino slot machines must give back a curtain percentage of money. If they are programmed suboptimally, they jsut spit out some cash after, say,  a series of five losses. Slot machines massively appeared in Russia in early 90's and I know a guy, who watched gambles and then played if they left the slot machine after a long series of losses.
2. The paradox with growing expectation is as follows: you make bets, each time doubling your stake until you win (and then you restart the process). If your capital is infinite can be arbitrary large, anyway, your profit in the end is (independent of ). And the expected number of bets before you win is just But can indeed largely deviate from the expectation and your limited wealth diminishes with each bet as follows: thus you will most likely go bankrupt very quickly, recall the blue scenario at Figure 3!