Eine Umfrage in der Facebook Gruppe "Trading and Education" hat gezeigt, dass man gegen Optionsscheine eine starke Abneigung hat. Hauptgrund war: "die Kurserstellung sei völlig untransparent". Obwohl man von den Optionsscheinen eher Finger weg halten sollte, ab und zu kann sich der Handel damit lohnen. Wir erklären die Risiken der Optionsscheine (Zeitwertverlust, hoher Geld-Brief Spread, Kursmanupulation) und bieten einen Simulator zur Einschätzung der möglichen Gewinne und Verluste an.
Optionsscheine sind die Surrogater der "wahren" Optionen. Theoretisch ist der Preis einer "wahren" Option durch den Black-Scholes Modell definiert. Eingabeparameter dieses Modell sind: aktueller Preis des Basiswertes, Strike, Zinssatz, Optionslaufzeit, Volatilität des Basiswerts und evtl. die Dividendenrendite. Sobald man diese Werte kennt, kann man theoretisch den Optionspreis berechnen. In der Praxis ist es aber nicht so. Grund dafür ist vor allem, dass die Volatilität des Basiswerts nicht konstant, sondern zufällig und zeitabhängig ist. Entsprechend, weichen die Optionsmarktpreise von den theoretischen Preisen ab und man vegleicht die Optionpreise im Sinne von sogenannter impliziter Volatilität, also der Vola-Wert, mit welchem das Black-Scholes Modell den Marktpreis der Option ausgibt.
Scherzend sagt man: Black-Scholes sei falsche Formel, in welche man falsche Vola eingibt um die richtigen Optionspreis zu bekommen.
In der Tat stimmt das:
1) Black-Scholes Modell nimmt konstante Vola und normalverteilte Renditen an, was ständig durch die Praxis widerlegt wird.
2) Auch die implizite Vola ist ein falsches Wert, allein deswegen weil sie nicht nur von Optionslaufzeit, sondern auch von Streik abhängen kann, was absurd ist.
3) Dabei ist der Marktpreis eines Options ein richtiger Wert.
Wie gesagt, sind die Preise der (liquiden) Optionen durch den Markt definiert. Anders ist aber im Fall der Optionsscheine. Deren Preise sind im wesentlichen durch den Marketmaker (also Emittenten) bestimmt. Klar sollte es die Regel vom Handelsplatz und BaFin geben, welche die Manipulationsmöglichkeit im Rahmen halten. Aber der Marketmaker kann, im Prinzip, die implizite Volatilität so einschätzen, wie es für ihn am besten ist. Auf liquidem Markt wäre es kaum möglich aber auf illiquiden Markt kann man das sehr wohl machen.
Zweites Problem ist es, dass die Option mit der Zeitablauf ihre [Zeit]wert verliert. Mit anderen Worten: im Unterschied zu den Aktien und Anleihen artbeitet die Zeit im Fall von Optionen gegen den Anleger!
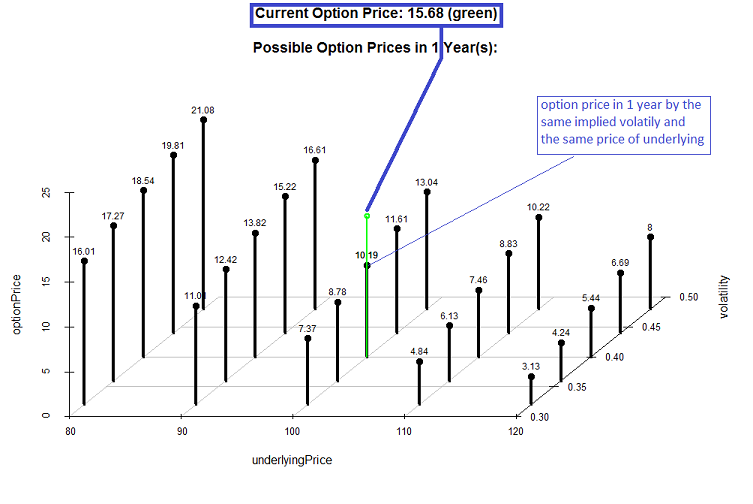
Um die Sensivität von Optionen zu den Basiswertbewegung, Änderung der impliziten Vola und der Zeitablauf einzuschätzen ist es hilfreich, die sogenannten Greeks (partielle Ableitungen der Black-Scholes Formel) zu verstehen. Zum Glück geht es auch ohne: mittels unseres Optionsszenariosimulators! Er zeigt, wie der Optionspreis in Zukuft aussieht, je nach Basiswertpreis, implizite Vola und Planungshorizont.
Im folgenden Video zeigen wir ein Case Study: Put auf Adidas. Zuerst merkt man eventuellen Trendumbruch, dann zu hohes KGV, sowie die niedrige implizite Vola. Also alles - chart, fundamentals und quant - sprechen für einen Put. Es bleibt nur die Szenarien mit unserem Optionsscheinrechner zu überprüfen.
Ein weiteres Problem is hoher Geld-Brief Spread. Nehmen wir an, man fixiert immer den Gewinn von +20% bzw. Verlust von -20%. Selbst wenn der Geld-Brief Spread "nur" 1% ausmacht (normalerweise ist er noch höher), muss man in 52,53% der Fälle gewinnen um lediglich den Break-even-Punkt zu erreichen! In der Tat: sei 
Allerdings kann sich der Handel mit den Optionscheinen ab und zu lohnen. Und zwar dann, wenn man seine Chancen, die Bewegung des Basiswerts richtig zu raten, sehr hoch einschätzt und wenn die implizite Volatilität niedrig ist. Aber auch dann muss sehr vorsichtig sein und nur mit kleineren Summen traden.
FinViz - an advanced stock screener (both for technical and fundamental traders)