Артиллерист-финансист и вездесущее нормальное распределение — letYourMoneyGrow.com

Сегодня, 23-го февраля, сам Бог велел поговорить о боге войны артиллерии. Всякий, кто хоть немного интересуется военным делом, знает, какую огромную роль она играет во время войны. Особо любознательные знают и знаменитые орудия и системы: "трехдюймовку", ЗиС-3, "Катюшу" (и немецкий Nebelwerfer), а из современного "Акацию" и "Гиацинт", минометы "Василек" и "Тюльпан" и прочий цветник.
Вероятностно-статистические методы в артиллерии обычно остаются в тени лоска парадов и грома боев. А между прочим именно они во многом и обеспечивают победу в бою. В этой статье мы перейдем от "Акаций" к акциям и поговорим о вездесущем нормальном распределении - чрезвычайно полезном как в теории стрельбы, так и в управлении инвестиционным портфелем.

Когда я проходил обучение по специальности "оптическая разведка в артиллерии", теории вероятностей (в приложении к теории стрельбы) нас особо не учили. Преподаватели ограничивались рассказами о том, как их мучили этой теорией в училищах (с намеком на то, что мы должны быть благодарны, что нас минует чаша сия). Я, однако, был любознательным студентом - и потому подобные разговоры лишь разжигали мое любопытство. Тем более что по основной специальности (экономика), какой-никакой теорвер нам преподавали. В результате с применением математических методов в артиллерии я познакомился по замечательному учебнику "Теория вероятностей" Елены Сергеевны Вентцель. Елене Сергеевне удалось почти невозможное - просто и понятно, но одновременно довольно глубоко и широко изложить весьма нетривиальный предмет. Оказалось, что теория стрельбы во многом опирается на (двумерное) нормальное распределение. В одномерном случае его плотность задается формулой

$f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$
а двумерном

$f(x_1,x_2) = \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}} \exp \left\{ -\frac{1}{2(1-\rho^2)}\left[ \frac{(x_1-\mu_1)^2}{\sigma_1^2}-\rho \frac{2(x_1-\mu_1)(x_2-\mu_2)}{\sigma_1\sigma_2} +\frac{(x_2-\mu_2)^2}{\sigma_2^2}\right] \right\}$
где $\mu_1, \mu_2$ - математические ожидания (средние значения), $\sigma_1, \sigma_2$ - дисперсии (меры рассеивания), а $\rho$ - коэффициент корреляции (взаимозависимости) случайных величин $x_1, x_2$ .
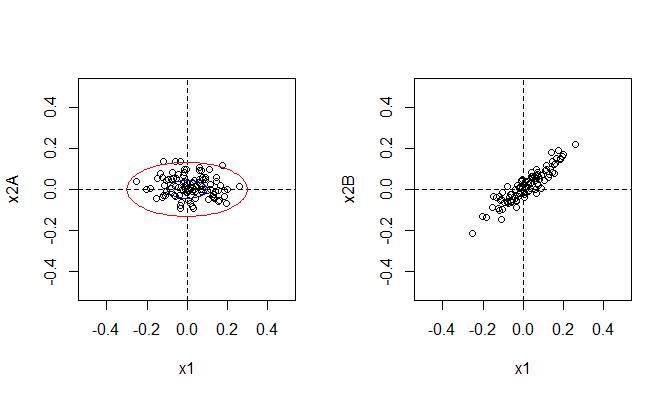
А что такое случайные величины $x_1, x_2$ ?! Well, в артиллерии это отклонения снарядов от (центра) цели по осям координат, а в финансах - доходности по составляющим портфеля (если наш портфель состоит из двух акций). В зенитной артиллерии нам понадобится уже трехмерное нормальное распределение, ну а в портфель и вовсе можно (хотя далеко не всегда нужно) напихать сколько угодно акций. Для всего этого разработан весьма подробный математический аппарат, но так далеко копать (от забора до обеда) мы не будем, ибо это уже двумерный случай весьма сложен. А можно проще?! Можно и нужно!

R - бесплатная программа статистического анализа - позволяет нам просимулировать по методу Монте-Карло выборку из случайной величины, распределенной по двумерному нормальному закону. Точнее, из двух таких величин - средние и дисперсии в обоих случаях одинаковы, а вот коэффициенты корреляции разные: в первом случае $\rho_A=0$ (т.е. $x1$ и $x2A$ независимы, а во втором $\rho_B = 0.7$ (что означает весьма сильную взаимозависимость $x1$ и $x2A$ ). Вот программный код на встроенном языке R

N=100
mu1 = 0.02
sigma1 = 0.1
mu2 = 0.01
sigma2 = 0.05
rhoA = 0.0
rhoB=0.7
x1 = rnorm(N, 0.02, 0.1)
x2A = rhoA * x1 + sqrt(1-rhoA*rhoA)*rnorm(N, mu2, sigma2)
x2B = rhoB * x1 + sqrt(1-rhoB*rhoB)*rnorm(N, mu2, sigma2)

library(plotrix)
par(mfrow=c(1,2))
plot(x1, x2A, xlim=c(-0.5,0.5), ylim=c(-0.5,0.5))
abline(h=0, v=0, lty=2)
draw.circle(0,0,sigma1,nv=100,border="blue",lty=1)
draw.circle(0,0,3*sigma1,nv=100,border="red",lty=1)
plot(x1, x2B, xlim=c(-0.5,0.5), ylim=c(-0.5,0.5))
abline(h=0, v=0, lty=2)

В деталях вникать в него при первом знакомстве с предметом необязательно, поясним только значения параметров. $N$ может означать как число трейдов (а в случае пассивных инвестиций - скажем, месяцев в течение которых мы держим порфель), так и число выпущенных по цели снарядов. Да-да, 100 снарядов - это еще мало, даже на одиночную цель (к примеру, установку ПТУР) при стрельбе с закрытых огневых позиций расходуют куда больше снарядов (хотя понятно, что для уничтожения такой цели достаточно одного прямого попадания). А по одиночным танкам вести стрельбу с закрытых огневых позиций вообще считается нецелесеобразным. Ибо когда ведут огонь с закрытых огневых позиций, снаряды попадают не точно в цель, а в эллипс рассеивания вокруг цели. В первом нашем случае (типичное) рассеивание составляет 100 метров (0.1 километра) по x1 и 50 метров (0.05 километров) по x2. Говоря проще - это продольное и боковое рассеивание (продольное обычно всегда больше - недолеты-перелеты). Так что осколки-то до цели долетят, а вот прямого попадания может и не быть. Поэтому-то по установке ПТУР стрелять смысл есть, а по танку смысла мало.
А иногда этот эллипс еще и смещен - если у орудия или прицела есть систематические погрешности. В нашем случае смещения составляют 20 и 10 метров. Но такие смещения обычно быстро корретируются при пристрелке. Ну а что же коэффициент корреляции?! При стрельбе его можно принять равным нулю, разве что сильный ветер дует под углом к направлению стрельбы, тогда преобладает снос, к примеру, вправо-вперед. А так продольное и боковое рассеивания друг от друга обычно не зависят.

А вот в случае с акциями корреляциями обычно пренебрегать нельзя - вот, к примеру, как выглядят дневные колебания курсов акций Даймлера и ДойчеБанка.

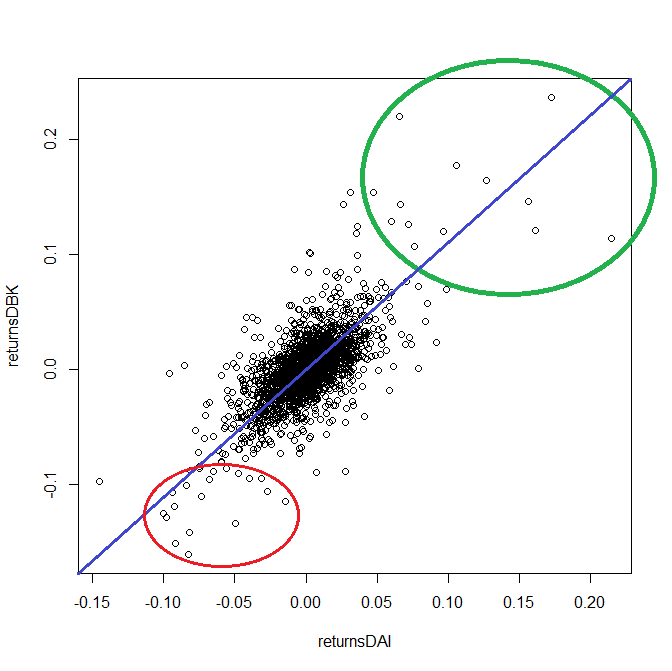
Сравните их с правым графиком на первом рисунке - не правда ли похоже?! По крайней мере если не считать аномалий на концах, обведенных зеленым и красным (но об этих аномалиях - в другой раз).

Ну и напоследок очень полезный практический пример. Наверняка вам приходилось слышать от оголтелых сторонников пассивного инвестировая, что надо каждый месяц покупать акции и держать их - мол, долгосрочно у такого портфеля есть только один путь - наверх. Что ж, для американского SPY и немецкого DAX это исторически верно (а вот для японского NIKKEI уже нет). Но допустим, что NIKKEI - это досадное исключение (восток - дело тонкое). Но тут есть нюанс - во-первых, мы делаем не большое разовое вложение, а накопительный план - каждый месяц понемногу (ибо много-то у большинства нет). А во-вторых, деньги нам нужны не через "абстрактный долгосрок", а через конкретный временной промежуток - обычно 10, 20 или 30 лет. Можно ли оценить ожидаемый доход и вероятность потерь таких накопительно-инвестиционных планов?! Да, можно, и тут нам опять поможет нормальное распределение, причем на этот раз хватит и одномерного.
Посмотрите, как четко плотность нормального распределения ложится на эмпирическую плотность распределения годовых доходностей по немецкому индексу DAX! А справа - так называемый QQ-plot - точки почти на одной прямой, что тоже говорит о том, что модель хорошо отображает эмпирические данные.

Ну а дальше запрограммировать симулятор сценариев - дело техники. И кстати, для немецкого DAX'а любопытные результаты он дает:

Срок инвест. плана	Вероятность потерь	Ожидаемая доходность	Медианная доходность
10 лет	20%	158%	141%
20 лет	15%	280%	224%
30 лет	8%	459%	340%

Так что, как видите, не бывает инвестиций без риска потерь, так же как не бывает без них войны. Но все-таки лучше "воевать" на бумаге, не так ли?! В бою (или с реальными деньгами) опыт дается дорого, а математика - это часть физики (и вообще любой науки), где эксперименты стоят дешево - так говаривал академик Арнольд.

P.S.
Сторонники Талеба, особенно те, что знакомы с его трудами лишь поверхностно, наверняка уже кипят от возмущения - мол, неправильно применять к моделириванию рынков нормальное распределение. Поясняем: для (внутри)дневной торговли, конечно, неправильно - о чем, в частности, свидетельствуют корреляционные аномалии и "тяжелые хвосты" на втором графике. Но для долгосрочного инвестирования, когда резкие падения и бурный рост сглаживают друг друга - вполне адекватно. Посмотрите еще раз на последний график, чтоб убедиться в этом.
Более того, наша задача - опровергнуть миф о безрисковом долгосрочном инвестировании. И уж если даже нормальное распределение показывает, что безрисковых инвестиций в рисковые активы не бывает, то задачу можно считать 100%-но выполненнной, ибо нормальное распределение - это самое оптимистичное, что можно предположить, отталкиваясь от реальных фактов.

Like this post and wanna learn more? Have a look at Knowledge rather than Hope: A Book for Retail Investors and Mathematical Finance Students

FinViz - an advanced stock screener (both for technical and fundamental traders)

Share this: