Gas Storage Fair Price | online Calculator

Remarkably, many market players in energy market still cannot calculate the fair value of a gas storage. In particular, many of them rely on perfect foresight. We put online a simple but correct model from QuantLib. Confidence intervals are estimated as well.

NB! This time not for retail investors but for the colleagues from energy industry. Have a look at short introductory video.

Gas Storage is a relatively complex option to evaluate, esp. if there are non-trivial constraints. Remarkably, many energy companies cannot correctly evaluate even the simplest storage contracts. Moreover, they often resort to a so-called perfect foresight: the price paths are considered random but once the price path is known, it is assumed to be known completely (like at the left-hand sketch).

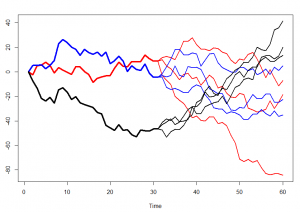Prefect foresight (unrealistic)	One-step foresight (realistic)

This is, of course, very simplistic assumption, a real life model should be something like the right-hand sketch: with each step we get more and more info about the path, however, we foresee it only until the next forking.

Klaus Spanderen did a great job evaluating the precision of the perfect foresight. Though it can be surprisingly good, another case shows that it should be considered with caution, namely as the highest upper bound of the fair storage value.

That's why a correct model (both in the sense of arbitrage free pricing and accurate numerical implementation) is necessary. However, there is another (very) big challenge: sensitivity to the market parameters estimation.
There is a simple model implemented in QuantLib. It relies only on the dynamics of the spot (day-ahead) gas price, assuming that its logarithm follows the Ornstein-Uhlenbeck process. The term structure of gas futures contracts is disregarded (s. remark), so there are just two parameters to estimate, namely, the speed of mean reversion and the volatility of (historical) gas spot price. In order to do this we use R package SMFI5. It implements an explicit method and a Fisher information to estimate the parameters. Without dwelling into details it worth noting that two method gives two different (though usually similar) point estimations. But the confidence intervals are wide and significantly depend on parameter estimation method!
Respectively, one should either implement an accurate and robust model or consider the model output not as the genuine storage value but rather as a milestone to check whether the market price is still im Rahmen or not.