Many investment funds and financial services that want your money argue with a deferred capital yield tax. For instance, in Germany if you trade by yourself, you immediately pay the capital returns tax [Kapitalertragsteuer] (unless the net result of your previous trades is negative). But if you invest in a fund, you don't pay the tax on returns until you sell your share (you still pay a tax on dividends).
We show that though, in general, an investor profits from tax deferral, one should not exaggerate its effect. Moreover, due to annual tax-exempt amounts [Jahresfreibetrag], an immediate taxation can be better than a deferred one.
Before 2009 a German investor could avoid the withholding tax, if kept the stock for more than one year. Nowadays one has to pay 26.375% yield tax (+church tax, if applicable). Normally, it is charged immediately from every profitable trade. The losses on trades with negative returns accrue in a so-called Verlusttopf (literally, a Loss-Pot). No taxes on profitable trades are charged as far as the Verlusttopf is not completely balanced with profitable trades. Verlusttopf can be carried over into the following year. Additionally, there are annual tax-exempt amounts: €801 for singles and €1602 for families.
Since many appeal to the tax deferral, let us evaluate its effect.
For simplicity let us assume equal annual return (e.g. this is more or less the case for a conventional pension insurance). Without a loss of generality let the initial wealth be equal to one. Denote the tax rate with
. If the yield tax is deferred than your terminal wealth in
years is
(check lesson 2 if you have troubles with this formula).
But if you pay tax in the end of each year, your wealth in a year is . In two years it is
. Analogously in
years it is
.
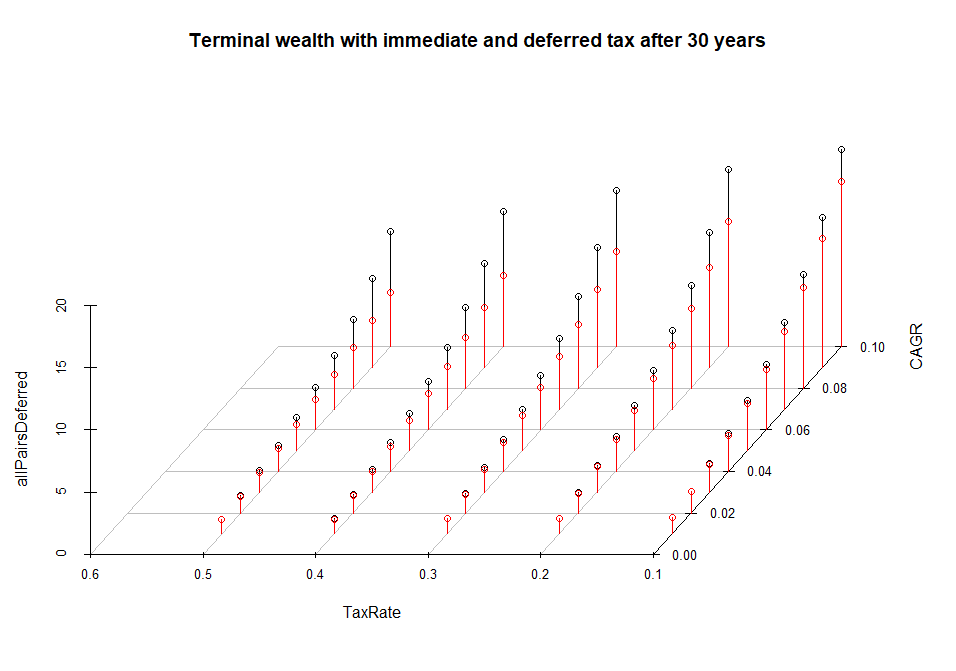
Since your wealth grows exponentially, the immediate taxation should be harmful. Exponential growth means: the larger your wealth the faster it grows and is a deduction from the wealth. However, the effect can be moderate even in the long term, as the chart above suggests. By a small CAGR the effect is really hardly distinguishable even if the tax rate is high and the investment period is long.
Thus the deferred tax argument likely makes sense if you are proposed to invest in a high-yield mutual fund for a long term. But it is really ridiculous in such cases like I experienced once: a Polish broker XTB told me that since their H.Q. is in Poland, they will not deduct the taxes immediately but rather send me a respective document for my tax declation in the end of year, thus I should profit from additional trading capital.
Moreover, the losses can be carried over into the next years but the annual exempt amounts cannot. Let us consider the case: a trader starts with €10000 trading capital (not untypical for novices) and generates 6% return each year (less typical for novices but finally the DAX grows 6%-7% in the long term). By the tax rate of 26.375% and exemption amount of €801 we get (check the original calculation in Excel)
| Year | Wealth by deferred Taxation | Wealth by immediate Taxation |
| 0 | 10000,00 | 10000,00 |
| 1 | 10600,00 | 10600,00 |
| 2 | 11236,00 | 11236,00 |
| 3 | 11910,16 | 11910,16 |
| 4 | 12624,77 | 12624,77 |
| 5 | 13382,26 | 13382,26 |
| 6 | 14185,19 | 14184,68 |
| 7 | 15036,30 | 15022,55 |
| 8 | 15938,48 | 15897,44 |
| 9 | 16894,79 | 16810,97 |
| 10 | 17908,48 | 17764,86 |
| Deferred Tax | 1874,60 | 0 |
| Terminal Wealth | 16033,88 | 17764,86 |
I. e. immediate taxation was - due to annual tax exempt amount - better than deferred! Of course a sales guy may say that you can each year sell and buy your share in an investment fund in order to make use of the exempt amount. Well, this will minimize taxes but not necessary maximize your wealth due to high bid-ask spread and sometimes Ausgabeaufschlag (agio, issue surcharge).
Thus - do take tax deferral into account - but do it properly!
R Code to generate the chart:
rets=seq(1:10)/100
tax = seq(1:5)/10
Nr = length(rets)
Nt = length(tax)
YEARS = 30
allPairsDeferred = array(0.0, dim=(Nr*Nt))
allPairsInstant = array(0.0, dim=(Nr*Nt))
CAGR = array(0.0, dim=(Nr*Nt))
TaxRate = array(0.0, dim=(Nr*Nt))
counter = 1
for(j in 1:Nr)
{
for(k in 1:Nt)
{
CAGR[counter] = rets[j]
TaxRate[counter] = tax[k]
allPairsDeferred[counter] = (1+rets[j])^YEARS - tax[k]*((1+rets[j])^YEARS - 1)
allPairsInstant[counter] = (1+rets[j] - rets[j]*tax[k])^YEARS
counter = counter + 1
}
}
library(scatterplot3d)
s3d <- scatterplot3d(CAGR, TaxRate, allPairsDeferred, main="Terminal wealth with immediate and deferred tax after 30 years", angle=240, box=FALSE)
s3d$points(CAGR, TaxRate, allPairsDeferred, type="h", col="black", lwd=1)
s3d$points(CAGR, TaxRate, allPairsInstant, type="h", col="red", lwd=1)
FinViz - an advanced stock screener (both for technical and fundamental traders)
